Most people who take a calculus course never really learn calculus. They have only a hazy grasp of how the pieces fit together. Sure, they might be able to tell you that the derivative of x^2 is 2x, but ask them why and you’ll get a blank look. They learned to mask their confusion with shortcuts, and their teachers never really checked to see if there was anything deeper.
This is a pity, and a mark of how we fail to teach calculus correctly. If students really learned calculus, they wouldn’t find it confusing. They’d find it shocking, instead. Calculus is unlike arithmetic, algebra, or geometry, and learning calculus is learning a whole new way to think about math.
Arithmetic can be understood by simply counting on your fingers. Geometry can be understood by drawing shapes in the sand (or on the blackboard). Basic algebra can be understood by replacing the numbers in our arithmetic with variables. All of these build off of real-world analogues.
Calculus is different. Calculus has paradoxes at its core, and understanding calculus means coming to grips with these paradoxes in a way that doesn’t have a real world analogue. This is a tall order. In fact, it’s so tall it took literally 2000 years to do so.
When Democritus and Archimedes first approached the integration part of calculus through geometry, they recognized the usefulness of it quickly. Have an irregular shape or parabola that you need to calculate the area of? You just divide it up into infinitely small triangles, and “exhaust” the area. It actually works pretty well.
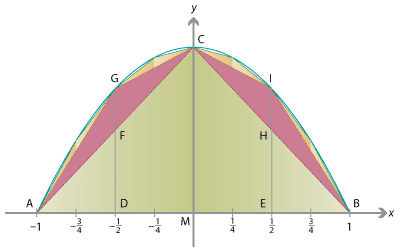
But what does infinitely small mean? The Greeks couldn’t figure it out. If they’re triangles, they presumably have an area. If they have an area, putting a bunch of them together should add up to some huge number, even if each one individually is small. If we say instead that they don’t have an area, putting a bunch together should add up to an area of zero. But somehow, calculus is supposed to tell us that putting an infinite number of triangles together adds up to a finite area.

This should be shocking. Our understanding of (Euclidean) geometry is almost entirely based on what we can draw. Integrative calculus looks like something we can draw on paper, but, when we try to, we end up with something that doesn’t really make sense. This very much disturbed the Greeks (and really disturbed the Jesuits as they followed in the Greek footsteps, to the point that the Jesuits declared “infinitesimals” heretical). What kind of geometry made less sense when you drew it out?
Understanding calculus from our other main method of understanding math, algebra, was even less fruitful at first. The Islamic Golden Age mathematicians, like Sharaf al-Din al-Tusi, experimented a lot with solving polynomials, and eventually realized they could find the maxima of certain functions by limits (note: that link goes to a clever recast of al-Tusi’s work into a modern day calculus word problem). But the use of that sort of “pure” algebra stops there. Without strict definitions of functions or limits, it’s hard to recognize a problem like “finding the maximum of a cubic polynomial” as what it is, which is finding the derivative of a function.
We had to literally extend algebra before we can get to derivative calculus from the other way. We needed functions, and the Cartesian coordinate plane, the latter of which was literally invented by Descartes and his academic descendants to help understand calculus (a fact which surprised me while researching this, given the standard math curriculum). If we understand functions and we have the coordinate plane, we can plot functions onto the coordinate plane. Then we can think about dividing up a parabola into line segments, and examining the slope of those line segments can get us thinking about how we might predict the way the slope changes over the course of a curve.
This is a useful trick. We can get to maxima and minima by looking at when the slope will reach zero. And, we’re at the point where we can be shocked again. It’s another paradox!
A smooth parabola can’t really be made of line segments. It’d end up being choppy. So the line segments would have to be infinitely small, and then we get the same issue as before. A parabola of definite length being made up of an infinite number of infinitely small line segments seems like a contradiction. Either they have a length, in which case the parabola is choppy, or they don’t, in which case they shouldn’t be able to “make up” anything.
So we’ve got paradoxes on either side of calculus. If we try to understand calculus by our old geometry, we’ve got a paradox of infinitely small triangles. If we try to understand calculus by our old algebra, we’ve got a paradox of infinitely small line segments. And yet both seem to work well for limited cases. How?
Ironically, pointing out these paradoxes of infinity can clue us into the greatest shock of all, which is that integrals and derivatives are two sides of the same coin. This is when calculus gets really surprising. The flip side of the rate of change of a parabola is the area under a parabola.
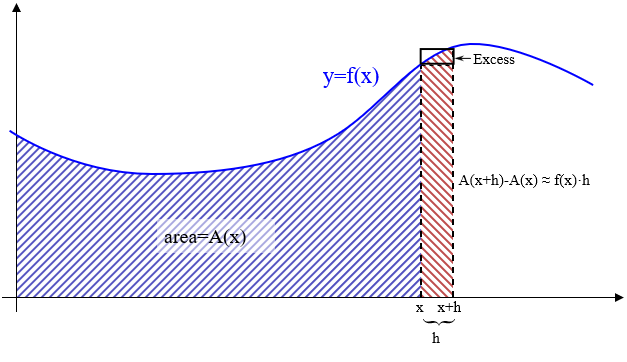
There is literally nothing in geometry and algebra so shocking as this. It’s so shocking that it took humanity 2000 years, from Democritus to Barrow (the first man to come up with a geometric proof of this) to realize this. Not only are geometry and algebra fundamentally related, but they’re related through something that’s both paradoxical and entirely physical (just think of the relation between total velocity and amount moved).
When students learn this, they should be like, “Holy shit, math! You mean that this entire time there’s been a deep relationship between two subjects I’ve been holding separate in my head? And now, armed with this new knowledge, I can go out and solve real world issues! That’s amazing!”
But, unfortunately, they’re not like that. I mean, I don’t know if any teenager would be caught dead being that enthusiastic about anything, but teachers don’t even attempt to make students that enthusiastic.
It’s not the teacher’s fault, either. The fault is in the curriculum. In this McGraw Hill textbook (which I think I used in my own AP Calculus class), this fundamental theorem of calculus is taught in chapter 4.5, sandwiched in between “The Definite Integral” and “Integration by Substitution”. So, students are taught how to do a derivative, how to do an integral, then “by the way these two seemingly unrelated topics are actually deeply related”, then “and also here’s another way to do integrals”.
Students react logically to this. They’re not shocked by the fundamental theorem of calculus, they’re confused. If it’s fundamental, why would it be stuck in the middle of another section? If they’re being taught both derivatives and integrals already, isn’t it obvious that they’re related as being part of calculus? It’s just another opportunity to zone out in math class.
That’s certainly how I remember feeling about it, and I was one of the best students in my high school math class. I didn’t care. I was too busy memorizing limits, differentiation, and integration tricks. When test day came, I had a bunch of formulae and equations in my head that I plugged in appropriately, and I scored the highest mark possible on both my AP Calculus exams.
I was so far into this mindset of “memorize techniques to score well on exams” that I don’t think a single lesson would have done anything, to be honest. To have really learned calculus well enough, I think I’d need to have been taught to appreciate the practical concerns that drove the development of calculus, as well as the understand the theoretical underpinnings of calculus.
If I were to teach a calculus class myself, those would actually be the main things I’d focus on. Memorization of formulae and techniques should be a small part of a calculus class, not the majority of it. Sure, it can make parts of calculus easier, but overreliance on it gives a “Chinese room” understanding of calculus. The student sees a problem and is able to put out the correct answer, but doesn’t really understand why the answer is correct. More importantly, if they see a similar problem formulated differently, they’re unable to solve it.
To handle the motivation portion, I’d start by introducing the practical concerns that drove the development of calculus. This could literally be a lab portion of the class. Bring out trebuchets for derivatives or make students try to fill a warehouse for integrals. Show them why people ever cared to calculate these values. But, most importantly, have them try to solve the practical problems first with just geometry and algebra, so they can appreciate the usefulness of calculus in the same way their academic ancestors did. These labs should motivate learning calculus, not illustrate it.
The theoretical underpinnings of calculus would, admittedly, be trickier. Having taught a lot of adults math, I am confident in saying that most students have an ok understanding of geometry and a poor understanding of algebra. This is because calculus is not the only math course that’s structured badly. Precalculus is, I dare say, even worse.
For those who aren’t familiar, precalculus is the American educational system’s way of bridging the gap between algebra and calculus. Instead of focusing on a deeper understanding of algebraic proofs and fundamentals, though, it’s a weird grab bag of introductions to some math that students are probably unfamiliar. So, a precalculus course introduces functions, polynomials, exponents, logarithms, trigonometry, and polar coordinates, in sequence, one after the other. And because the course is explicitly not about teaching calculus, the only clue that students get as to why they’re taught this is “you’ll need it later”.

What kind of student could learn 6 disparate pieces of math, one after another, in a mostly disconnected fashion, then start the next year and apply them all to calculus? Well, in my experience, pretty much none of them. They fail to learn functions, get confused why they’re learning the rest of it, and then start calculus having forgotten algebra but still not understanding precalculus.
A calculus course, then, has to take into account that a lot of students won’t have the right background for it. In that case, I’d say the entire first semester or so should be dedicated to a proper theoretical background for calculus: finding areas with geometry, functions, algebraic proofs, and at last the Cartesian coordinate plane to unite algebra and geometry. This would provide a clear theoretical transition into calculus (and theoretical motivation for calculus with proper foreshadowing).
Then derivatives and integrals can be covered in the second semester, with add-ons like exponents and logarithms, polar coordinates, and infinite series saved for either a follow-up course or for advanced students. The actual calculus section of the course would likely be similar to this excellent MIT textbook, actually.
A calculus course taught this way would, hopefully, make deep sense to the students. They’d begin with developing the background to calculus, ending the first semester with the same background that Newton and Leibniz had when they developed calculus.
Then the second semester could provide that shocking, “Aha!” moment. Students would not just get the knowledge of Newton and Leibniz, but get some small sense of what it must have been like to be them as they made their groundbreaking discoveries.
It took me a long time to appreciate math, and calculus longest of all. I only realized in college that I had been cheated out of a deep understanding of math and given a shallow collection of tricks instead. The education system focuses so much on the utility of math, even when it’s a reach (see the derivatives of trigonometric functions). It should focus on the beauty, the shock, and the awe instead.