Note: this essay is outside of my comfort zone, so there might be a few mistakes. I relied a lot on this paper and Wikipedia to help me think about it. Mistakes are my own.
The 1987 paper “Self-organized criticality: An explanation of the 1/f noise”, by Bak, Tang, and Wiesenfeld has 8612 citations. That is an astonishingly high number for a paper that presents a model for statistical mechanics. Even more astonishing is the range of papers that cite it. Just in 2020, it’s been cited by a paper on brain activity as related to genes, a paper on the “serrated flow dynamic” of metallic glass, and a paper on producing maps of Australian gold veins.
It is an incredibly influential paper on a huge variety of subjects. I mean, I doubt the scientists who wrote those papers have a single other citation in common in their whole research history. How did they all end up citing this one paper? What’s been the effect on science of having this singular paper reach across such a wide range of subjects?
These are the topics that I want to explore in this paper. Before I can, though, we have to start by explaining what the paper is and what it tries to be.
Self-organized criticality. or SOC, is a concept coming out of complexity science. Complexity science is generally the study of complex systems, which covers a really broad range of fields. You might remember it as the stuff that Jeff Goldblum was muttering about in Jurassic Park. When you get a system with a lot of interacting parts, you can get some very surprising behavior coming out depending on the inputs.
Bak, Tang, and Wiesenfeld, or BTW, were physicists. They knew that there were some interesting properties of complex systems, namely that they often displayed some similar signals.
For one, if you measure the activity of complex systems over time, you often see a 1/f signal, or “pink noise”. For instance, the “flicker noise” of electronics is pink noise, as is the pattern of the tides and the rhythms of heart beats (when you graph them in terms of frequency).
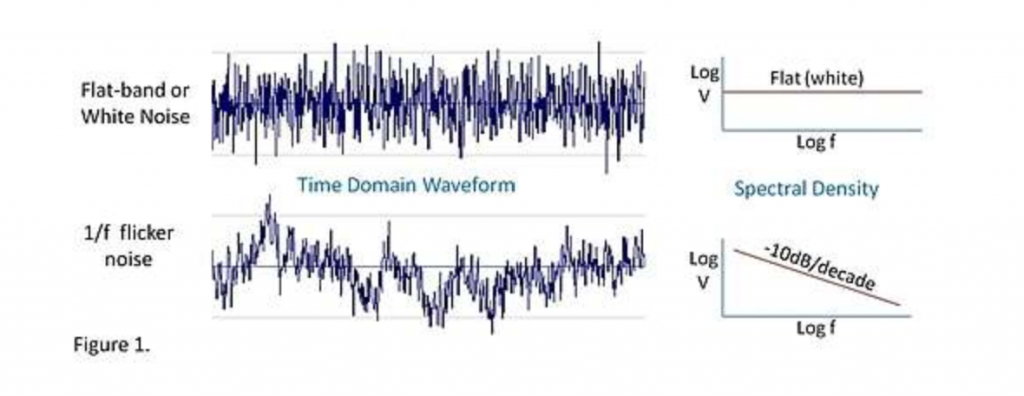
For another, if you measure the structure of complex systems over space, you often see fractals. They’re present in both Romanesco broccoli and snowflakes.

BTW proposed that these two are intimately related to each other, which had been suggested by others before. However, the way they proposed was that both can come from the same source [1]. In other words, 1/f noise and fractals can be caused by the same thing: criticality.
Criticality distinctions
Criticality is a phenomenon that occurs in phase transitions, where a system rapidly changes to have completely different properties. The best studied example is with water. Normally, if you heat water, it’ll go from solid, to liquid, to gas. If you pressurise water, it’ll go from liquid to solid (this is really hard and requires a lot of pressure).
However, if you both heat and pressurize water to 647 K and 22 MPa (or 700 degrees Fahrenheit and 218 times atmospheric pressure), it reaches a critical point. Water gets weird. At the critical point (and in the vicinity of it), water is compressible, expandable, and doesn’t like dissolving electrolytes (like salt). If you keep heating water past that, it becomes supercritical, which is a whole different thing.
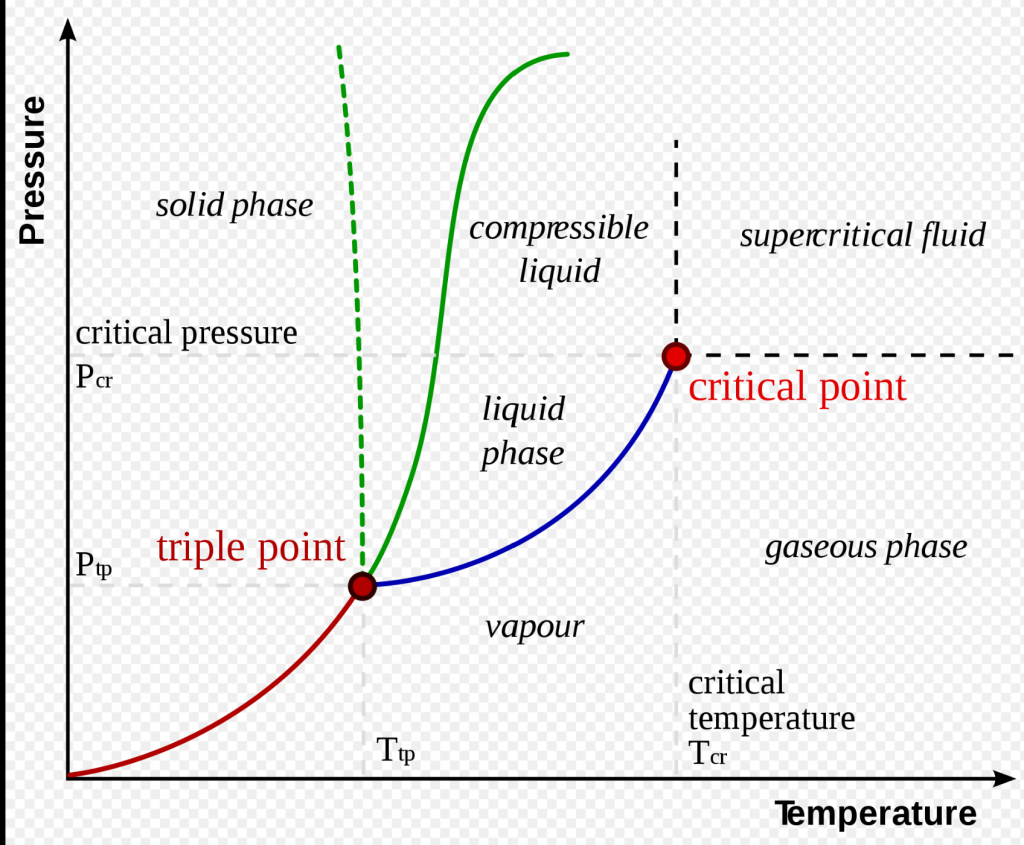
So, there are two important things about criticality. First, the system really rapidly changes characteristics within a very close vicinity to the parameters. Water becomes something totally unlike what it was before (water/gas) or after (supercritical fluid). Second, the parameters have to be very finely tuned in order to see this. If the temperature or pressure is off by a bit, the criticality disappears.
So what does that have to do with 1/f noise and fractals? Well, because systems are scale invariant at their critical point. That means that, if you graph the critical parameters (i.e. the things that allow the system to correlate and form a coherent system, like electromagnetic forces for water), you should always see a similar graph, no matter what scale you’re using (nano, micro, giga, etc.). This is different from systems at their non-critical point, which usually are a mess of interactions that change depending on where you zoom in, like the electromagnetic attractions shifting among hydrogen and oxygen molecules in water.

This is suggestive of fractals and 1/f noise, which are also scale invariant. So, maybe there can be a connection that can be explored.
Before BTW could make that connection stronger, though, they needed to fix the second important thing about criticality: the finely tuned parameters. 1/f noise and fractals are everywhere in nature, so they can’t come from something that’s finely tuned. To go back to water, you’re never going to see water just held at 647 K, 22 MPa for an extended period of time outside of a lab.
This is where BTW made their big step. What if, they asked, systems didn’t have to be tuned to the parameters? What if they tuned themselves? Or, to use their terminology, what if they self-organized?
Now, for our water example, this is clearly out of the question. Water isn’t going to heat itself. However, not every phase transition has to be solid-liquid-gas. It just needs to involve separate phases that are organized and can transition (roughly). Wikipedia lists 17 examples of phase transitions. All of these have critical points. Some of them have more than one.
So BTW just needed to find phase transitions that could be self-organized. And they kind of, sort of, did. They created a model of a phase transition that could self-organize (ish) to criticality. This was the sandpile model.
It goes like this: imagine dropping grains of sand on a chessboard on a table. When the grains of sand get too high, they topple over, spilling over into the other squares. If they topple over on the edge, they fall off the edge of the table. If we do this enough, we end up with an uneven, unstable pile of sand on our chessboard.
If we then start dropping grains randomly, we’ll see something interesting. We see a range of avalanches. Most of the time, one sand grain will cause a small avalanche, as it only destablizes a few grains. Sometimes, that small avalanche causes a massive destabilization, and we get a huge avalanche.
What BTW consider important about this model is that the sandpile is in a specific phase, namely heaped on a chessboard. This phase is highly sensitive to perturbations, as a single grain of sand in a specific spot can cause a massive shift in the configuration of the piles.
If you graph the likelihood of a massive avalanche vs. a tiny one, you get a power law correlation, which is scale invariant. And, most importantly, once you set up your initial conditions, you don’t need to tune anything to get your avalanches. The sandpiles self-organize to become critical.

So, with this admittedly artificial system that ignores physical constraints (i.e. friction), we get something that looks like criticality that can organize itself. From there, we can try to get to fractals and 1/f noise, but still in artificial systems. Neat! So how does that translate to 8600 citations across an incredibly broad range of subjects?
Getting to an avalanche of citations for SOC
Well, because BTW (especially Bak, the B), weren’t just going to let that sit where it was. They started pushing SOC hard as a potential explanation for anytime you saw both fractals and 1/f noise together, or even a suggestion of one or both of them.
As long as you had a slow buildup (like grains of sands dropping onto a pile), rapid relaxation (like the sand avalanche), power laws (big avalanches and small ones), and long range correlation (the possibility of a grain of sand in one pile causing an avalanche in a pile far away), they thought SOC was a viable explanation.
One of the earliest successful evangelizing attempts was in an attempt to explain earthquakes. It’s been known since Richter that earthquakes follow a power law distribution (small earthquakes are 10-ish times more likely to happen than 10-ish times larger earthquakes). In 1987, around the same time of SOC, it became known that the spatial distributions and the fault systems of earthquakes are fractal.

From there, it wasn’t so far to say that the slow buildup of tension in the earth’s crust, the rapid relaxation of an earthquake, and the long range correlation of seismic waves meant SOC. So Bak created a model that produced 1/f noise in the time gap between large earthquakes, and that was that! (Note: if this seems a little questionable to you, especially the 1/f noise bit, read on for the parts about problems with SOC).
Next: the floodgates were open. Anything with a power law distribution was open for a swing. Price fluctuations in the stock market follow a power law, and they have slow-ish build-up and can have rapid relaxation. Might as well. Forest fire size follows a power law, and there’s a slow buildup of trees growing then a rapid relaxation of fires. Sure! Punctuated equilibrium means that there’s a slow buildup of evolution, and then a rapid evolutionary change (I guess). Why not?
Bak created a movement. He was very deliberate about it, too. If you look at the citations, both the earthquake paper and the punctuated equilibrium paper were co-written by Bak. They were then cited and carried forward by other people in those specific fields, but he started the avalanche (if you’ll forgive the pun).
And he didn’t stop with scientific papers, either. He spread the idea to the public as well, with his book How Nature Works: the science of self-organized criticality. First of all, hell of a title, no? Second of all, he was actually pretty successful with this. His book, published in 1996, currently has 230 ratings on Goodreads. For a wonky book from 1996, that’s pretty amazing!
That, in a nutshell, is how the paper got to 8600 citations across such a broad range of fields. It started off as a good, interesting idea with maybe some problems. It could serve as an analogy and possibly an explanation for a lot of things. Then it got evangelized really, really fervently until it ended up being an explanation for everything.
But what about science?
This brings us back to our second question, which is: what have the effects on science been of this? Well, of course, good and bad.
Let’s discuss the good first, because that’s easier. The good has been when SOC has proved to be an interesting explanation of phenomena that didn’t have great explanations before. For example, this paper, which I relied on heavily in general for this essay, discusses how SOC has apparently been a good paradigm for plasma instabilities that did not have a good paradigm before.
Now, I completely lack any knowledge of plasma instabilities, so I’ll have to take their word for it, but it seems unlikely that the plasma instability community would know of SOC without Per Bak’s ceaseless evangelism.
The bad is more interesting. Any scientific theory of everything is always going to have gaps. However, most of them never have any validity in the first place. Think of astrology, Leibniz’s monads, or Aristotle’s essentialism: they started off poorly and were evangelized by people who didn’t really understand any science in the first place.
SOC is more nuanced. It had and has some real validity and usefulness. Most of the people who evangelized and cited it were intelligent, honest people of science. However, Bak’s enthusiastic evangelism meant that it was pushed way harder than the average theory. As it was pushed, it revealed problems not just with how SOC was applied, but with a lot of the way theory is argued in general.
The first and most obvious problem was with the use of biased models. This is always a tough problem, because not everything can be put in a lab or even observed. There is always a tension between when a model is good enough, and what things are ok to put in a model or leave out. But Bak and his disciples clearly created models that were designed to display SOC first of all, and only model the underlying behavior secondarily.
Bak’s model of punctuated equilibrium is a particularly egregious example. Bak chose to model entire species (rather than individuals), chose to model them only interacting with each other (ignoring anything else), and modeled a fitness landscape (which is itself a model) on a straight line. In more straightforward terms, his model of evolution is dots on a line. Each dot is assigned a number. When the numbers randomly change, they are allowed to change the dots around them too with some correlation.
This is way, way too far from the underlying reality of individuals undergoing selection. It makes zero sense, and was clearly constructed just to show SOC. Somehow, though, it got 1800 citations.
However, I feel less confident criticizing Bak’s model of earthquakes. In this, he models earthquakes as a two dimensional array of particles. When a force is applied to one particle, it’s also applied to its neighbors. Now, obviously earthquakes are 3-dimensional, and there is a wave component to them that’s not well-represented here, but this seems like an ok place to start.
Maybe it’s not though. Maybe we should really start with three dimensions, and model everything we know about earthquakes before we call an earthquake model useful. Or maybe we should go one step further, and say an earthquake model is only useful once it’s able to make verifiable predictions. Newton’s models of the planets could predict their orbits, after all.

A purist might hold that models aren’t useful until they’re predictive, but that’s a tough stance for people actually working in science. They have to publish something, and waiting until your model can make verifiable predictions means that people won’t really be communicating any results at all. Practically speaking, where do we draw the line? Should we draw the line at any model which is created to demonstrate a theory, but allow any “good faith” model, no matter how simplistic?
A different sort of issue comes up with SOC’s motte-and-bailey problem. Bak, in his book How Nature Works, proposed SOC for lots of things that it doesn’t remotely apply to. Punctuated equilibrium was just one example. When he was pressed on it, he’d defend it by going back to the examples that SOC was pretty good on.

It’s not a problem to propose a theory to apply to new situations, of course. However, so many theorists rely on the validity of a theory for a limited example to justify it for a much broader application, rather than defending it for the broader application.
On one level, that’s just induction: recognizing the pattern. However, it’d seem that there should be much more effort put into establishing that there is a pattern, and then justifying the new application as soon as possible.
This ties into the next problem: confusing necessary and sufficient assumptions. In the initial paper, BTW were pretty careful about their claim. SOC was sufficient, but not necessary, to explain the emergence of fractals and 1/f noise. It was necessary, but not sufficient, to have power law distribution, long range correlations, slow buildup with rapid relaxations, and scale invariance to have SOC [2].

When Bak was hunting for more things to apply SOC to, he got sloppy. He would come close to making claims like fractals and 1/f noise implied SOC, or power laws implied SOC. Now, this is maybe ok at a preliminary part of the hunt. If you’re looking to find more applications of SOC, you have to look somewhere, and anything involving fractals, power laws, or the like is an ok place to start looking. But you can’t make that implication in your final paper.
Not only does this make your paper bad, but it poisons the papers that cite it, too. This is exactly what’s happened with some of the stranger papers that have cited BTW, which is another reason for its popularity besides Bak’s ceaseless evangelism and its validity for limited cases. SOC got involved in neurology through this paper, which uses a power law in neuronal avalanches to justify the existence of criticality. In other words, it says a power law is sufficient to assume criticality, and then goes from there to create a model which will justify self-organization.
But that’s backwards! Power laws are necessary for criticality; they aren’t sufficient. Power laws show up literally everywhere, including in the laws of motion, the Stefan-Boltzmann equation for black body radiation, and the growth rate of bacteria. None of those things are remotely related to criticality, so they obviously can’t imply criticality. The paper, which is cited 454 times (!), is based on a misunderstanding.
SOC is actually kind of a unique case, scientifically, because it did lay out its necessary and sufficient hypotheses so clearly. That’s why I can point out the mistake in this paper. However, many more less ambitious scientific hypotheses aren’t nearly so clear. For example, here’s the hypothesis of the neurology SOC paper, copy pasted from the abstract: Here, we demonstrate analytically and numerically that by assuming (biologically more realistic) dynamical synapses in a spiking neural network, the neuronal avalanches turn from an exceptional phenomenon into a typical and robust self-organized critical behaviour, if the total resources of neurotransmitter are sufficiently large.
The language is a bit dense, but you should be able to see that it’s unclear if they think SOC is sufficient and necessary for neuronal avalanches (you have to have it), or just sufficient (it’s good enough to have it). In fact, I’d wager that they wouldn’t even bother to argue the difference.
It’s only because SOC is such an ambitious theory and Bak tried to apply it to so many things that he was forced to be so clear about necessary vs. sufficient. Way, way too often in scientific papers suggestive correlations are presented, and then the author handwaves what exactly those correlations mean. If you present a causal effect, is that the only way the causal effect can occur? Are there any other ways?
The weighing
So, in conclusion, the bad parts of SOC’s incredible wide-ranging influence are a lot of the bad parts of scientific research as a whole. Scientists are incentivized professionally to publish papers explaining things. That’s one of the big purposes of scientific papers. They are not particularly incentivized to be careful with their explanations, as long as they can pass a sniff test by their peers and journal editors.
This means that scientists end up overreaching and papering over gaps constantly. They develop biased models, over-rely on induction without justification, and confuse or ignore sufficient and necessary.
BTW’s impact, in the end, was big and complicated. They created an interesting theory which had an enormous impact on an incredible variety of scientific fields in a way that very few other theories ever have. On most of the fields, SOC was probably not the right fit, although it may have drove the conversation forward. On a few of the fields, it was a good fit, and helped explain some hitherto unexplained phenomena. On all of the fields, it introduced new terms and techniques that practitioners were almost certainly unfamiliar with.
It’ll be interesting to see when the next theory of everything comes about. Deep learning and machine learning are turning into a technique of everything, which comes with problems of its own. Who knows?
Footnotes
1. This is where some of the problems and the ubiquity of SOC come from. Bak, in particular, has come very close to suggesting they always come from the same source, which is way more indefensible than they can come from the same source. See the motte and bailey discussion further on.
2. Quick primer on sufficient and necessary: Sufficient means that if you have SOC, you are guaranteed to have fractals and 1/f noise, but you don’t need to have SOC to have those. Necessary means you needed power laws, etc. for SOC, but you might also need more things too for SOC